Why is music is the way it is? You might know the song “do re mi”, which laid out the notes most commonly used as the building block for western music.
Let’s take a listen of the notes “do re mi fa so la ti do”, of which most of us should be familiar with.
These sequence / collection of notes is also called “scales”, or specifically western scale. Pretty much all songs are an arrangement of notes from a scale.
If we think critically, how do they come to be? If history were repeated, will we have the same scales, or at least something similar?
I think it’s a yes, and the reason is actually pretty simple, we just want to make “nice sounds”. How does “sound” become “nice”? The “sound” we are referring to here are “notes”, which is referring to a “pitch” or a “frequency”. And we want to have some notes that sounds nice together.
And I think nice “sounds” happens in nature as well. We can take the example of bird songs, for example this Great Tit bird:
We can try to musicalize the Great Tit bird song:

Or we can also listen to this Cuckoo:
The cuckoo sound is actually quite similar to door bell:

To me, both the bird sounds and the instrument sounds are both pleasing to the ear, and I believe it applies to everyone as well from all ages.
So, what make these sounds nice? First we have tone quality. A tone has good quality if it has a clear “fundamental” pitch. For example, the bird whistle is quite clear tone, meanwhile other sound like the sound of waterfall rushing or TV white noise doesn’t have a clear tone to it. However, that’s not our main focus for now, maybe on another post.
For now, let’s assume our sound source has a clear tone. And we only focus on the pitch, that is the frequency of the note.
Let’s start simple, below is a single 440 HZ sine wave tone. (headphone warning! start with low volume)
Sine wave will be simple:
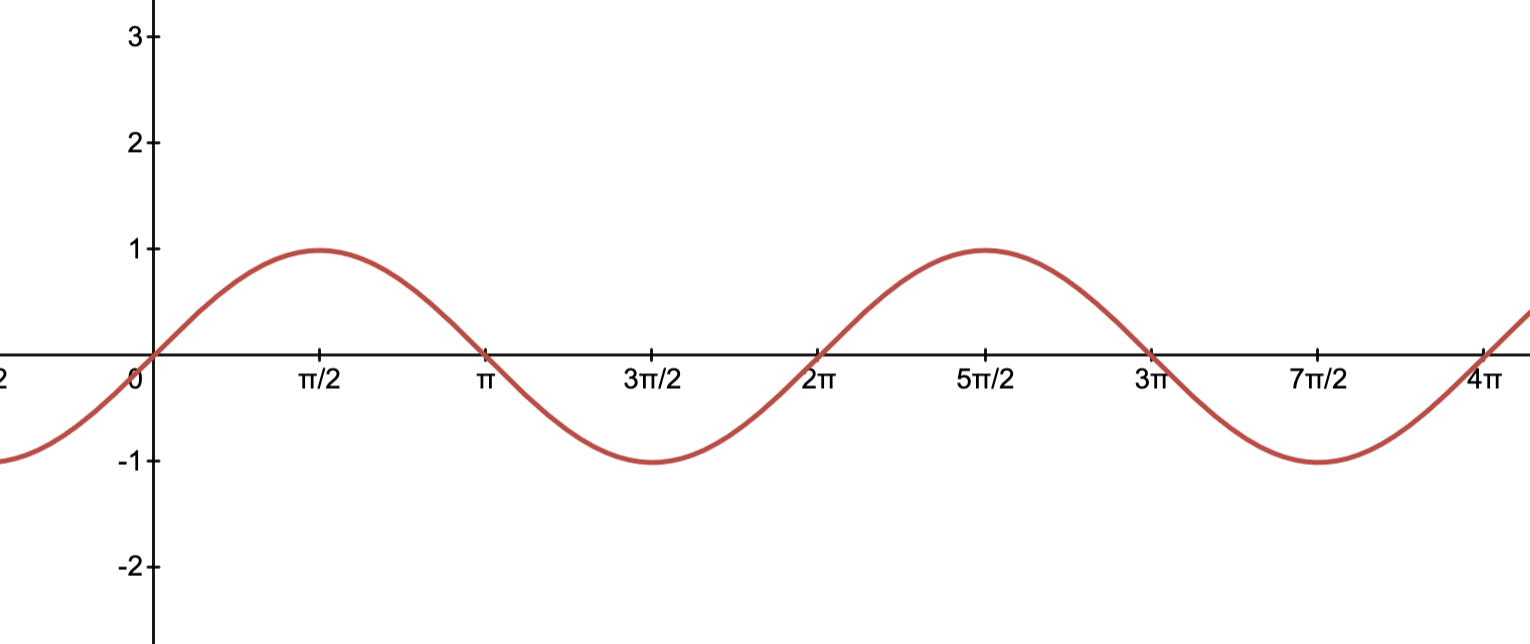
Now let’s find another note that has a relation to it. The simplest relation is the tone with double frequency, 880hz. For every complete cycle done by the 440Hz tone, the 880Hz tone would’ve done two complete cycle.
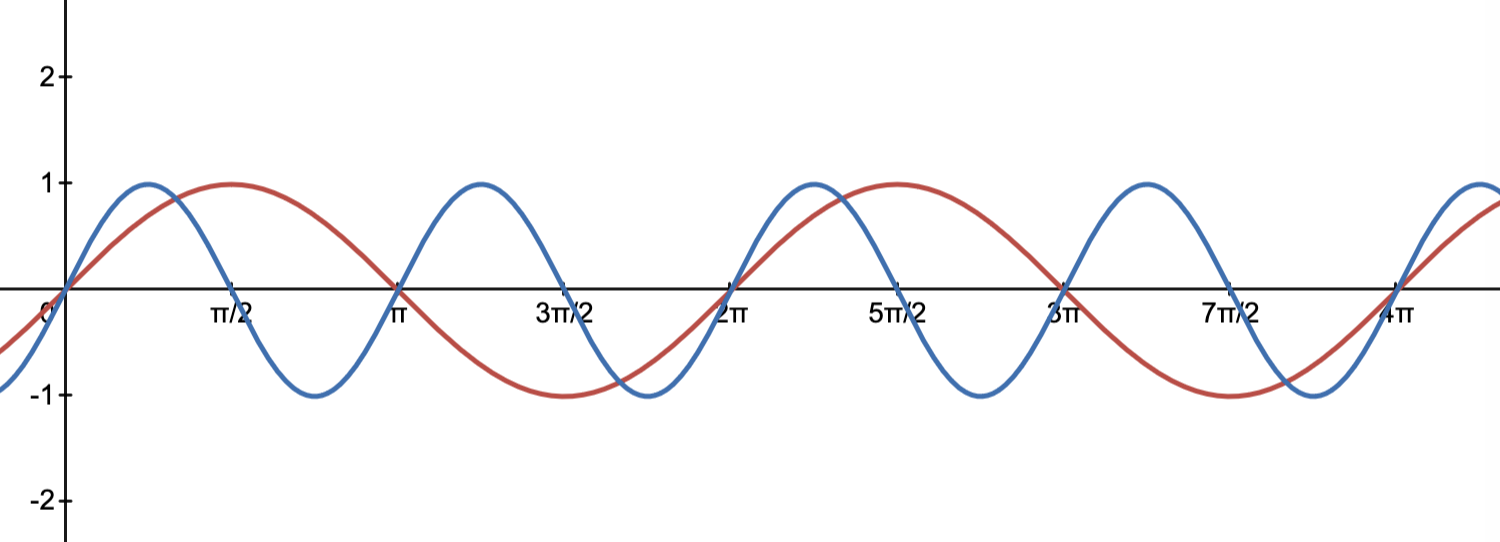
Here’s how it sounds like, it is offset a bit so we can tell the difference
Maybe it doesn’t sound particularly “nice” to you, or at least, it’s nothing artistic. So for contrast, maybe let’s see what happen if it’s not “nice”. Let’s pick something off from 880hz, like 850hz. As we can see in the graph, it seems to just go on by itself without any relation with each other.
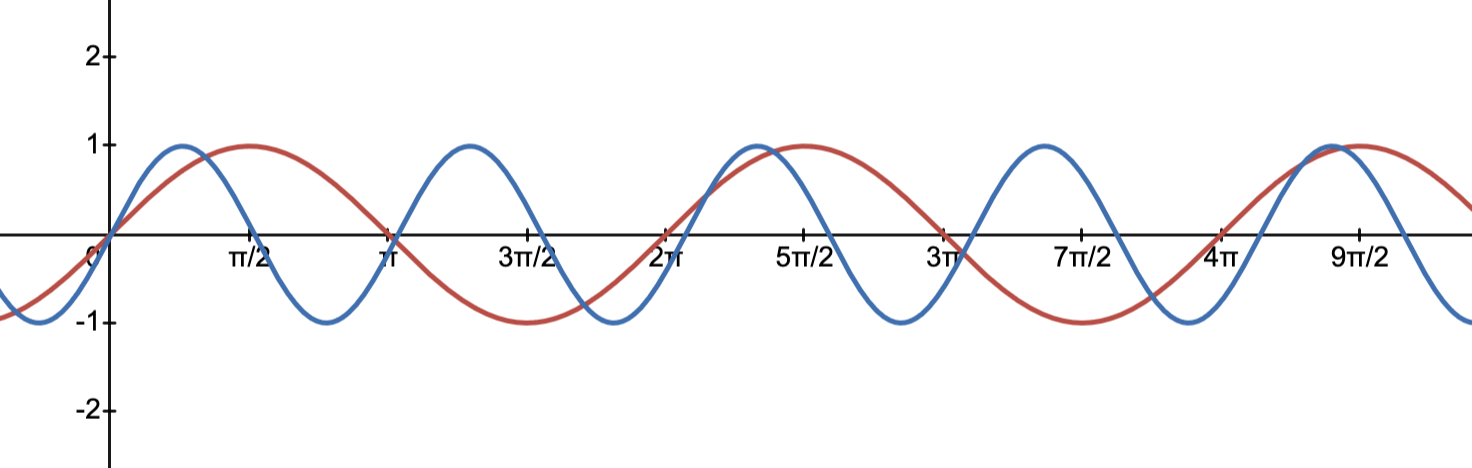
And it sounds pretty dissonant too.
Ok, so go back to our 440Hz & 880Hz example. They have the ratio of 2:1. This is called the octave. Let’s try other ratio, 3:1 might be obvious, however, actually 3:2 is more fundamental since 3:1 is like an octave higher than 3:2. So let’s try 3:2.
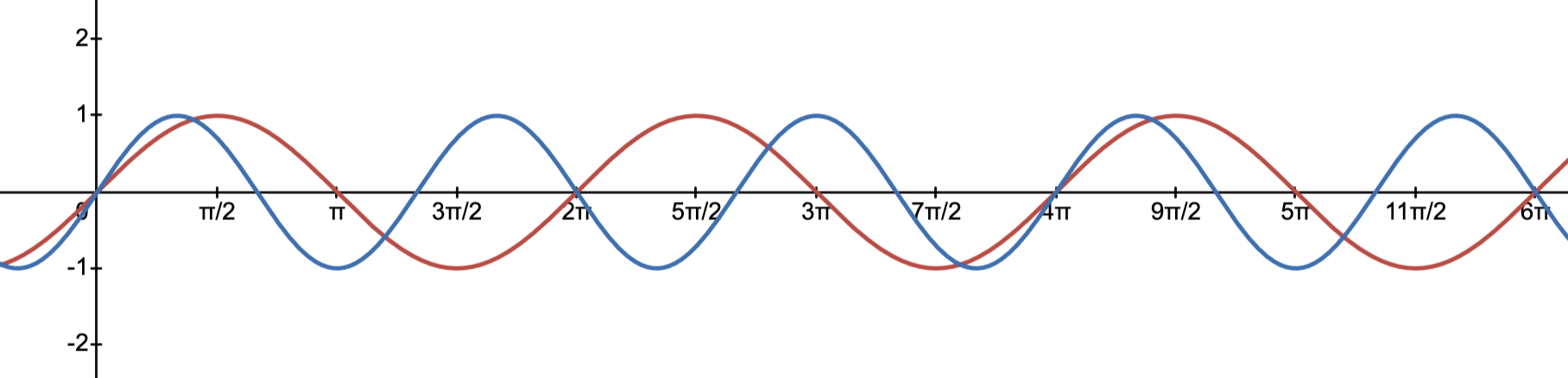
It should sound quite nice! And there’s a name to this interval / ratio as well. It’s called “perfect fifth”. Fifth because it’s the fifth note in the scale.
Let’s do 4:3? In fact, 4:3 is very closely related to 3:2, it’s just flipped then times two.
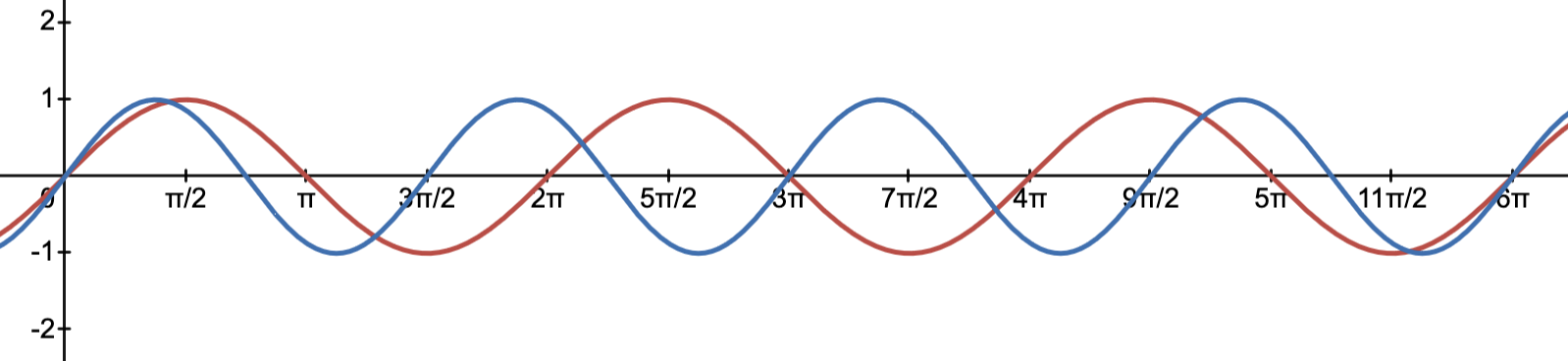
This is 4:3 relation is also called “perfect fourth”.
How about 5:4?
This is actually called “major third”. This is the interval that is used by the Cuckoo bird!
And 6:5, is “minor third”,
Minor third might sound slightly more “wobbly” or distorted to you. But it should sound relatively ok.
This interval is sung by the Great Tit bird.
If we go along, it starts to become more dissonant (less harmonious). This is makes sense because the “meeting point” between the two sine-waves become further and further apart (their lowest-common-multiple is higher).
Here is 7:6,
Here is 8:7,
Here is 9:8,
So, we have gathered some intervals:

I will also introduce the concept of “steps”.
If you are not familiar with piano keys, each of the nearest note (white and black) is 1/2 step apart. So in the diagram below, the major third interval is: 1/2 + 1/2 + 1/2 + 1/2 = 2 step apart. As you can see below.
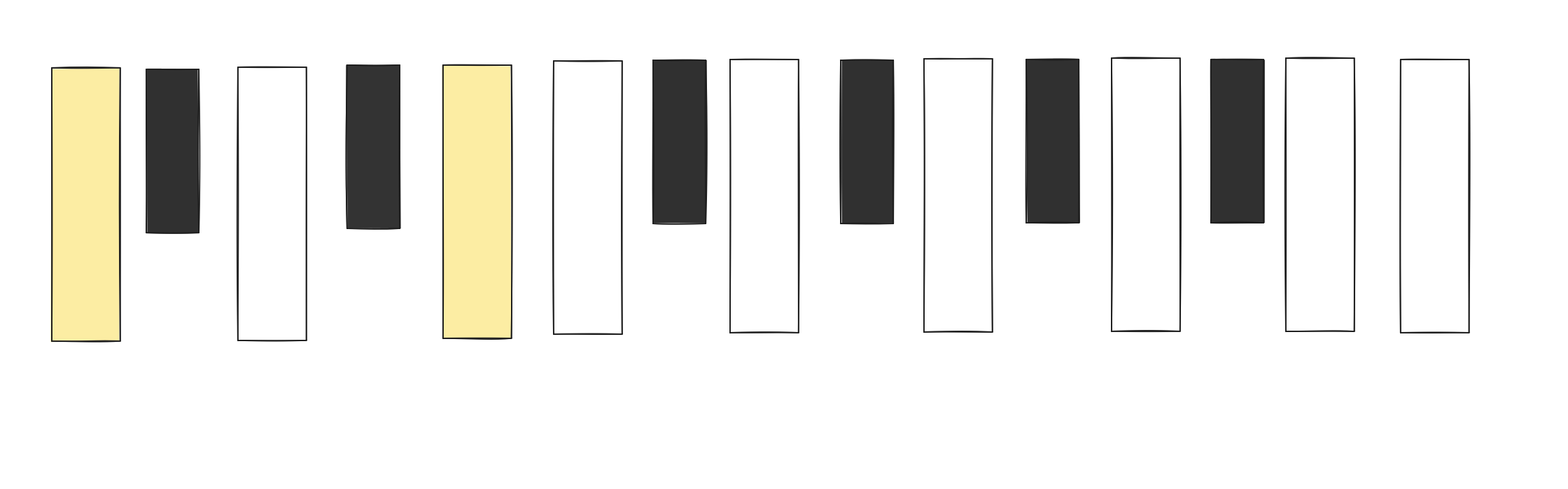
So for other intervals, minor third is 1.5 steps, perfect fourth is 2.5 steps, perfect fifth is 3.5 steps.
Using these “steps”, we can easily compose intervals; that is applying an interval to a note that has another interval with another note.
For example: a perfect fifth is 3.5 step apart. Major third is 2 step apart. Minor third is 1.5 step apart. We can notice that:
3.5 = 2 + 1.5
So by right composoing major third and minor third should get us perfect fifth. Let’s check the frequency ratio:
(Major Third) 5/4 * (Minor Third) 6/5 = 6/4 = 3/2 (Perfect Fifth)
So we get 3:2, which is a perfect fifth!
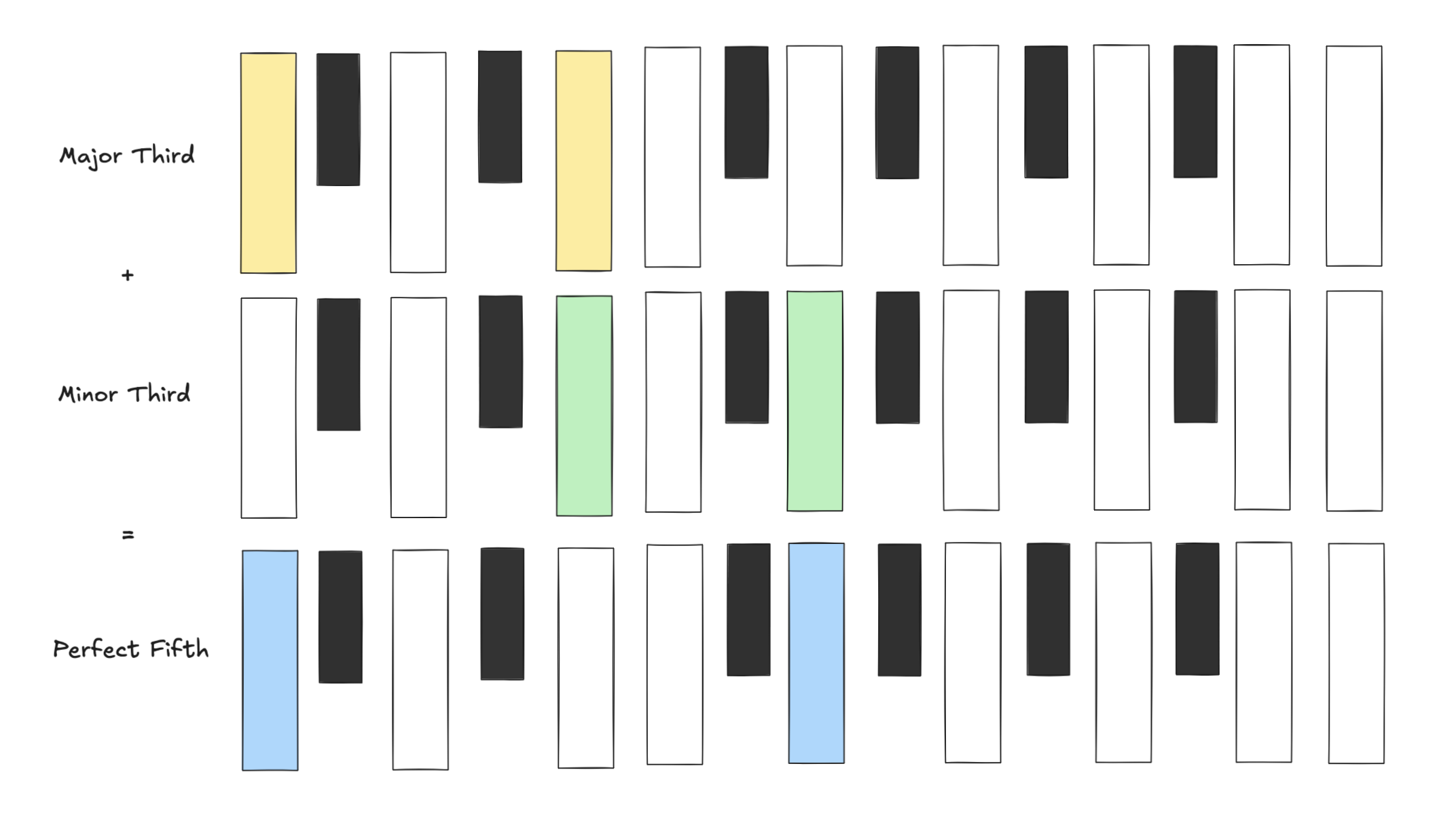
That’s great! How about other intervals?
Surprisingly, or sadly, it doesn’t always work. Let’s try this sequence of composing:
- go up perfect fifth (3/2), plus 3.5 step
- go down perfect fourth (1 / (4/3) == 3/4), minus 2.5 step
- go up perfect fifth (3/2), plus 3.5 step
- go down perfect fourth (1 / (4/3) == 3/4), minus 2.5 step
If we calculate the steps, we should net (3.5-2.5) + (3.5-2.5) = 2 steps, which is a major third.
Let’s check the frequency ratio, major third should have 5:4, which is 1.25. However, when we check the multiplication of the frequency ratio from the composition: we get 3/2 * 3/4 * 3/2 * 3/4 = 81/64 = 1.265625 which is not quite the same thing. You can compare the sound:
Actual 5/4:
81/64:
The difference is very subtle, but if you can notice it, 5/4 sounds ever-so-slightly more pure and 81/64 sounds ever-so-slightly distorted.
So this is the sad truth, we can’t really easily make music with perfect intervals because otherwise it might keep slowly-slowly diverting.
So people come up with a solution called “equal temprament”. In this solution, the octave (2:1), is equally split to 12 half-steps. So one step is equal to the ratio of 2^(1/12) ~ 1.05946309436.
This way we can get the existing intervals:
| Interval Name | Perfect Ratio | Equal Temprament Ratio | Off by |
|---|---|---|---|
| Minor Third | 6/5 = 1.2 | 2^(3/12) = 1.189207115 | -0.9% |
| Major Third | 5/4 = 1.25 | 2^(4/12) = 1.259921049 | +0.8% |
| Perfect Fourth | 4/3 = 1.33.. | 2^(5/12) = 1.334839854 | +0.4% |
| Perfect Fifth | 3/2 = 1.5 | 2^(7/12) = 1.498307076 | -0.1% |
Piano is tuned like this (sort-of, I’m not sure exactly, not a piano technician haha), so it can work well for all the different keys & scales, with only small deviation for each note.
For more, can read https://en.wikipedia.org/wiki/Equal_temperament. You can also play with this online tone generator: https://onlinetonegenerator.com/multiple-tone-generator.html?utm_source=chatgpt.com . There should be a lot of interesting videos on youtube explaining these concepts as well.
Fun fact:
Air raid siren also make use of these intervals. On one video by Matthias Wandel referenced below, he make the sirene using two concentric wheels, one with 6 “flaps” and one with 10 “flaps”


This means we have interval of 10:6 = 5:3. We didn’t have it on our original discussion, but it’s basically 6:5, with the 6 divided by 2 (means it’s one octave lower). This is also called a “major sixth” interval.
Highly recommended to watch the video:
~ Thanks for reading! ~